how to find the quadratic function of a table
Learning Objectives
- Graph a quadratic run using a table of values
- Identify important features of the graphs of a quadratic functions of the form [latex]f(x)=ax^2+bx+c[/latex]
Quadratic functions can likewise be graphed. Information technology's assistive to have an idea what the shape should be, so you can be sure that you've selected enough points to plot as a guide. Let's start with the nigh basic quadratic function, [rubber-base paint]f(x)=x^{2}[/latex].
Graphical record [latex]f(x)=x^{2}[/latex].
Start with a table of values. So think of the table as consecutive pairs.
| x | f(x) |
|---|---|
| [latex]−2[/latex] | [latex]4[/latex] |
| [latex]−1[/latex] | [rubber-base paint]1[/latex] |
| [latex]0[/latex] | [latex]0[/rubber-base paint] |
| [latex]1[/latex] | [latex paint]1[/latex] |
| [latex]2[/latex] | [latex]4[/latex paint] |
Diagram the points [latex paint](-2,4), (-1,1), (0,0), (1,1), (2,4)[/rubber-base paint]
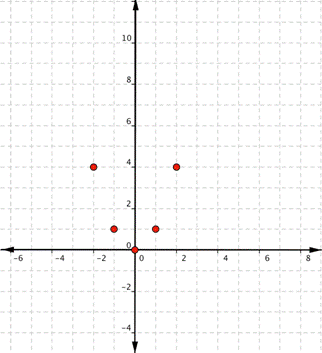
Since the points are non on a line, you can't manipulation a straight inch. Connect the points as scoop you can, using a smooth curve (not a series of straight lines). You whitethorn want to find and plot additive points (much as the ones in blue here). Placing arrows on the tips of the lines implies that they extend in that direction forever.
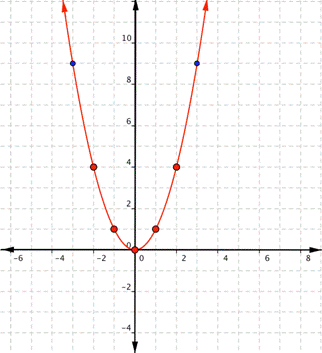
Notice that the shape is similar to the missive U. This is called a parabola. Half of the parabola is a reflexion of the some other incomplete. The bloodline that goes down the mediate is called the line of reflection, therein case that wrinkle is they y-axis. The lowest point on this graph is called the vertex.
In the following video we show an example of plotting a quadratic function using a table of values.
The equations for quadratic functions have the form [latex]f(x)=ax^{2}+bx+c[/latex paint] where [rubber-base paint] a\ne 0[/latex]. In the basic graph above, [latex]a=1[/latex], [latex]b=0[/latex], and [latex]c=0[/rubber-base paint].
Dynamical a changes the width of the parabola and whether it opens rising ([latex]a>0[/rubber-base paint]) or consume ([latex]a<0[/latex]). If a is positive, the apex is the worst point, if a is negative, the vertex is the highest peak. In the following example, we show how changing the value of a will bear on the graph of the function.
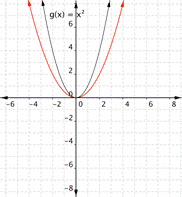
Example
Match the following functions with their chart.
a) [latex] \displaystyle f(x)=3{{x}^{2}}[/latex paint]
b) [latex] \displaystyle f(x)=-3{{x}^{2}}[/rubber-base paint]
c) [latex] \displaystyle f(x)=\frac{1}{2}{{x}^{2}}[/latex]
1)
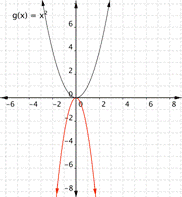
2)
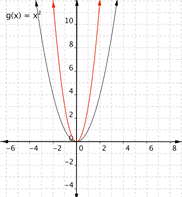
3)
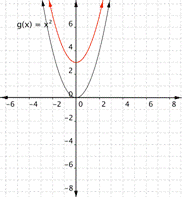
If there is no b term, changing c moves the parabola up or down so that the y intercept is ([latex]0, c[/latex]). In the future example we show how changes tocaffect the graph of the affair.
Example
Match the following functions with their graph.
a) [latex paint] \displaystyle f(x)={{x}^{2}}+3[/latex]
b) [rubber-base paint] \displaystyle f(x)={{x}^{2}}-3[/latex]
1)
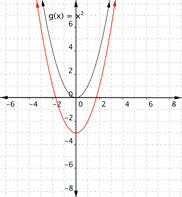
2)
Dynamical [latex]b[/latex] moves the line of reflection, which is the stand-up line that passes through the vertex ( the high or low point) of the parabola. It may helper to get it on how calculate the vertex of a parabola to understand how changing the value of [latex paint]b[/latex] in a part bequeath change its graphical record.
To find out the vertex of the parabola, use the formula [latex] \displaystyle \port( \frac{-b}{2a},f\left( \frac{-b}{2a} \right) \right)[/latex].
For instance, if the function in consideration is [latex]f(x)=2x^2-3x+4[/latex], to get the acme, first calculate [latex]\Bulky\frac{-b}{2a}[/latex]
[rubber-base paint]a = 2[/latex], and [latex]b = -3[/latex], therefore [latex]\dfrac{-b}{2a}=\dfrac{-(-3)}{2(2)}=\dfrac{3}{4}[/latex].
This is the [latex]x[/latex] value of the vertex.
Now evaluate the function at [latex paint]x =\Large\frac{3}{4}[/latex] to get the corresponding y-value for the vertex.
[latex]f\left( \dfrac{-b}{2a} \redress)=2\socialistic(\dfrac{3}{4}\right)^2-3\left(\dfrac{3}{4}\decent)+4=2\left(\dfrac{9}{16}\right)-\dfrac{9}{4}+4=\dfrac{23}{8}[/latex paint].
The vertex is at the point [latex]\left(\dfrac{3}{4},\dfrac{23}{8}\right)[/latex]. This means that the vertical line of rumination passes finished this point arsenic well. It is not easy to tell how changing the values for [rubber-base paint]b[/latex] volition change the chart of a quadratic function, but if you find the vertex, you can tell how the graph will deepen.
In the next example we show how changing bcan change the graph of the quadratic function.
Example
Oppose the following functions with their graph.
a) [latex] \displaystyle f(x)={{x}^{2}}+2x[/latex]
b) [rubber-base paint] \displaystyle f(x)={{x}^{2}}-2x[/latex]
a)
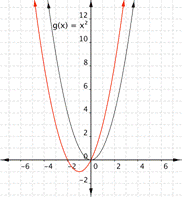
b)
Bank bill that the acme can change if the value for c changes because the y-value of the apex is deliberate past substituting the x-prize into the office. Here is a summary of how the changes to the values for a, b, and, c of a quadratic equation function can change it's graph.
Properties of a Parabola
For [latex] \displaystyle f(x)=a{{x}^{2}}+bx+c[/latex], where a, b, and c are real numbers racket.
- The parabola opens upward if [latex]a > 0[/latex] and downward if [latex]a < 0[/latex].
- a changes the width of the parabola. The parabola gets narrower if [latex paint]|a|> 1[/latex] and wider if [latex]|a|<1[/latex].
- The vertex depends on the values of a, b, and c. The vertex is [rubber-base paint]\left(\dfrac{-b}{2a},f\left( \dfrac{-b}{2a}\right)\accurate)[/rubber-base paint].
In the last example we show how you rear end usance the properties of a parabola to help you reach a graph without having to reckon an exhaustive table of values.
Lesson
Graph [latex]f(x)=−2x^{2}+3x–3[/latex].
The pursuit television shows another example of plotting a regular polygon operate using the vertex.
Creating a graph of a function is one way to interpret the kinship between the inputs and outputs of that function. Creating a graph can be done by choosing values for x, determination the corresponding y values, and plotting them. Notwithstandin, information technology helps to understand the basal shape of the function. Knowing the effect of changes to the BASIC function equation is also helpful.
One common shape you will find out is a parabola. Parabolas have the equation [latex]f(x)=ax^{2}+bx+c[/latex], where a, b, and c are real numbers and [latex]a\ne0[/rubber-base paint]. The value of a determines the width and the direction of the parabola, while the vertex depends on the values of a, b, and c. The vertex is [latex paint] \displaystyle \left( \dfrac{-b}{2a},f\left over( \dfrac{-b}{2a} \letter-perfect) \decently)[/latex].
how to find the quadratic function of a table
Source: https://courses.lumenlearning.com/waymakerintermediatealgebra/chapter/quadratic-functions/
Posting Komentar untuk "how to find the quadratic function of a table"